| Japanese | English |
2004年8月9日加筆
今回も、前回に引き続き、再分析を行います。最後に加筆します。
(オリジナル)
今回は航空自衛隊小牧基地からの戦闘機離陸です。
| 測定日時 | 2002年2月27日 12:55 |
| 天 候 | 曇り |
| 気 温 | 18℃ |
| 湿 度 | 48% |
| WAVEファイル: |
  |
 |
屋外の騒音レベルは48~50dBで、私の住んでいる名古屋市東区の国道41号線の近くより3dBは騒音レベルが低いです。
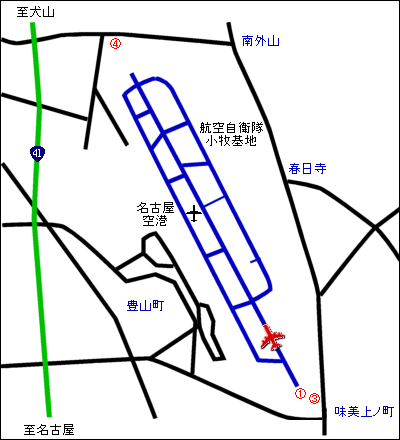
20秒18 左上の機体が戦闘機です。練習機T4かF4ファントムでしょうか?

21秒01

21秒29

22秒05

この4枚の画像はたった1秒47の間のものです。あまりに速くて追いきれませんでした。音量も最大で、普通騒音計のdBA表示で118dBAまでぶっ飛びました。
空き地の角です。最初の写真のすぐ左です。

その角から左です。この方角に滑走路、そのずっと左側に航空自衛隊の基地があります。

システムの無信号時のピークレベルメーター表示。
飛行機がいないときの通常の騒音を分析。49dBAくらい。
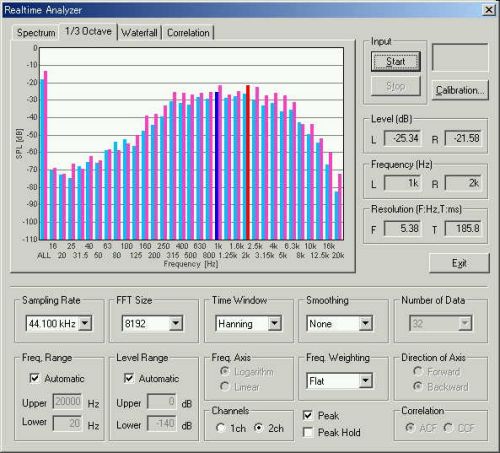
戦闘機のちょうど斜め前あたりでの1/3オクターブ分析図。
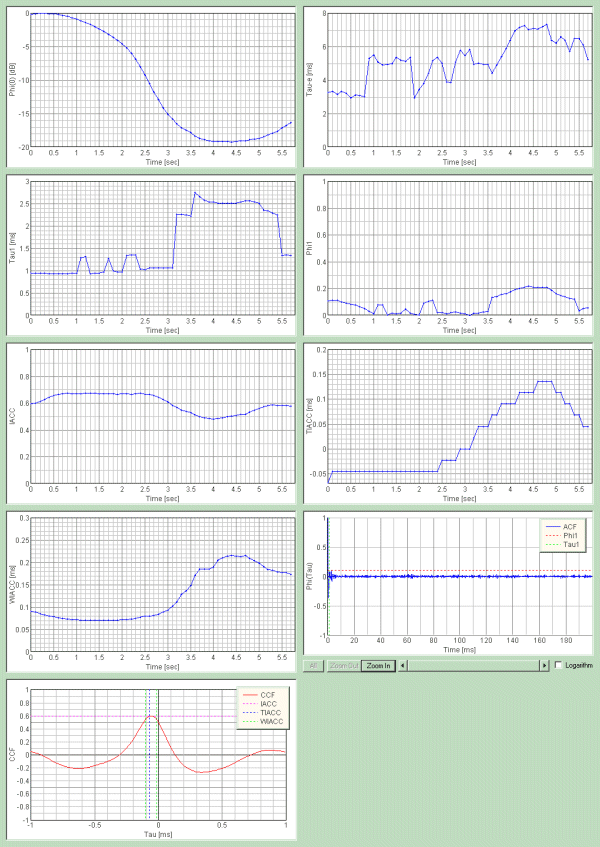
特徴的なリアルタイムな自己相関グラフ表示
ジェット旅客機着陸のときのも良く似ています。
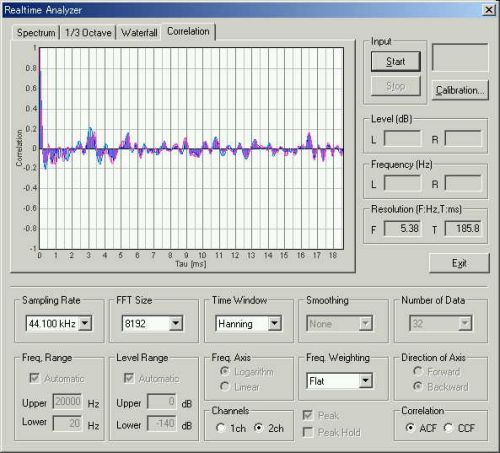
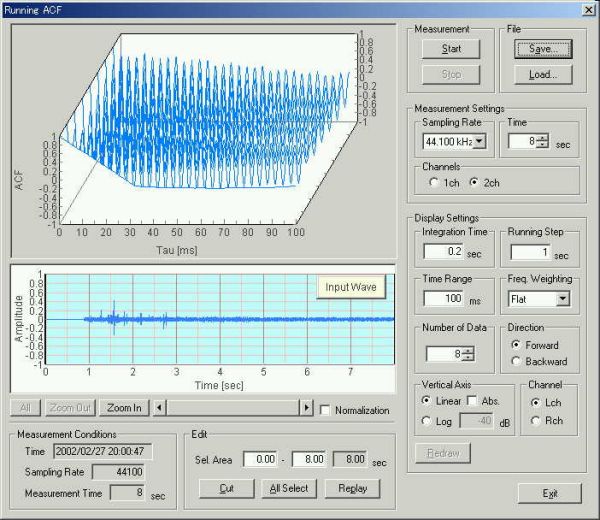
8秒間のランニングACF測定、積分時間0.2秒。下の図は音量ですが、近づいてきて、真横でマイクを追いかけましたが音量が弱くなっています。
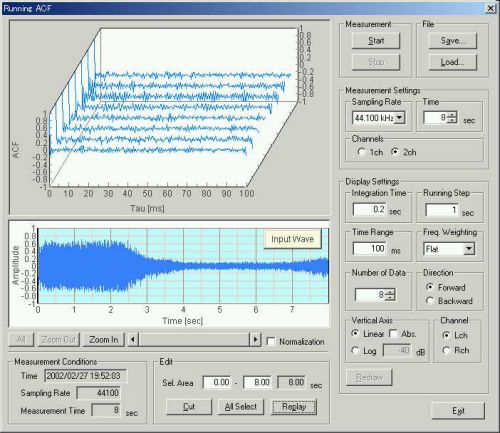
SAに読み込んで
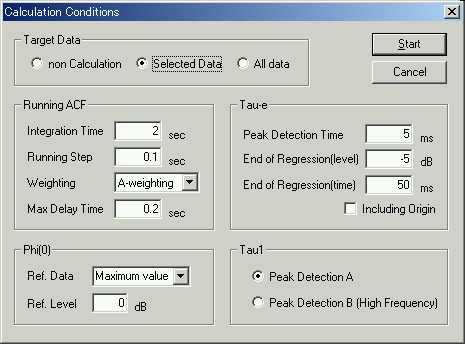
積分時間2秒で計算。約3分かかって計算終了。
Φ(0)音量の時間推移のグラフ。
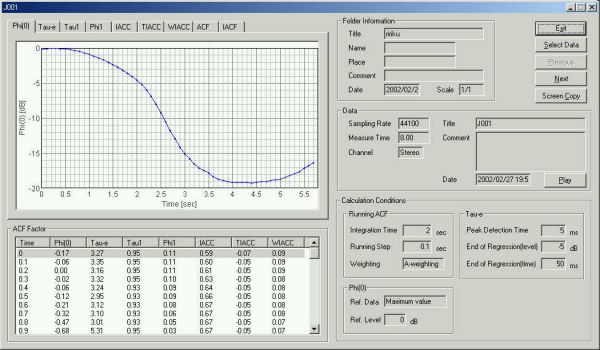
自己相関、2chの相互相関から得られる分析値の時間推移のグラフこれは右上のスクリーンコピーからワンクリックで画像化できます。これらのデータ解析の計算に3分かかっていたのです。
ジェット旅客機の着陸ときと同じで、近づいてくるときのτ1は0.95msで一定。最も接近して遠ざかるときは、2.5msでほぼ一定。これは後部ジェット噴射の排気音を遠ざかるときは受けるからです。
通過直後に118dBAをアコーの騒音計が記録しました。同じ位置でジャンボジェットは105dBAでした。滑走路をいっぱい使うために、低い位置で相当な迫力でした。とにかくうるさいです。この戦闘機は近くの自動車もきしむような、吹っ飛ぶような音波でした。
τIACCは斜め左からきた戦闘機が計測後3.1秒後に脇を通過し、4.9秒後に、マイクがそちらに追いかけかけています。
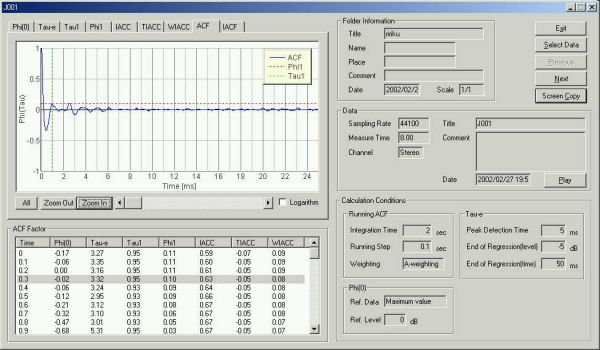
計測経過後0.3秒後、τ1 0.95m秒のときのACFグラフ
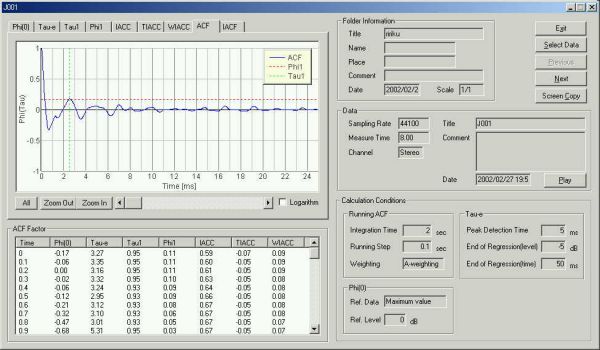
計測経過後4秒後 、τ1 2.5m秒のときのACFグラフ
2004年8月9日加筆分開始
まずRAのランニングACF画面で、実際の音を再生してみます。
このデータは全体的にクリアでいい録音です。ジェット戦闘機が突然離陸していきました。こちらの測定場所は滑走路の一番先の滑走路脇です。実際Replayボタンを押して再生してヒアリングしてみると、ジェット戦闘機自体の撮影が遅れたため、測定開始後2秒で、ジェット戦闘機は真横を通過していきます。その後2秒から4秒で急速におとが小さくなるのは、左チャンネルのマイクの指向性です。このランニングACFのWAVEのモニターは左チャンネルだけですが、マイクの前をジェット戦闘機が、左から右に移動した場合、このようなWAVEの表示になります。上空にあがり、7秒くらいにマイクが向きを変えてから左のマイクにも音が取れるようになってから、音圧レベルが大きくなっています。ヘッドフォーンSONYのMDR-200をDELLのINSPIRON8200二接続して、ヒアリングします。大変クリアです。生の音とは比較になりませんが、実際のWAVEデータには、迫力の秘密が入っているはずです。
というのは、ジェット戦闘機の音は、すごいのです。今回も隣を通り抜けていったときにすごい衝撃波を感じました。もう少し速度が音速に近いとあるいは音速よりはるかに速いと、車の窓ガラスが割れるというのも、理解できるほどです。
まず、さしあたって雑音や、まずい場所を調べるために、測定3に行ったように、拡大のための虫眼鏡のプラスボタンをクリックして、32倍に拡大してその場所を調べてみましたが問題ありません。
積分時間0.01秒の高周波の分析を行います。計算条件は同じです。
下の図のWAVE表示で左のマイクは測定開始後2秒までが大きくて、右のマイクは測定開始後2秒以降が大きい、これを解釈してみると、実際にその音を聞いてみてもステレオマイクの前を戦闘機が左から右に走り去ったのがわかります。
そしてこれが、上のグラフで、赤線で、指定された区間、測定開始後2.18秒から、0.01秒の区間のスペクトラム分析です。左右のスペクトラムから、左CHはやく350Hz、1.1KHz1.4KHz、2KHz、、、、7KHZまでのピークを持ち、低い周波数から、高い周波数まで、まんべんなく広範囲な周波数成分を持っています。
τ1のグラフです。このグラフをX軸方向に拡大せずに通常で、見た場合、縦の線が連続して、積分時間2秒のときのような、それぞれの時間や、連続した周囲がY軸の値として大体同じような値をとる点を結んだ線のグラフとは大きく違った縦の線Xj軸方向に重ねていったような動きの激しい外観です。この場合は大体Y軸の最大最小の幅もτ1のとる値として、目安として意味があります。
積分時間0.01秒の分析の場合にも、ジェット戦闘機の代表周波数は高い周波数成分は、Y軸の値が小さいほう、1.5msecは660Hz,1msec は1KHz、0.5msecは2KHz、0.3msecは3.3Khzを意味します。低いほうの周波数成分は、1.8msec 550Hz、1.6msec 630Hz、3msec 330Hz 、2.7msec 370Hz です。それらの範囲の代表周波数成分がマイクとジェット戦闘機の位置の関係で、変化します。
代表周波数は人間が聞いたときの音質に極めて等価の値です。通常は積分時間2秒で求めます。積分時間0.01秒の場合はピッチ(音の高さ)という語であらわしたほうが適切かもしれませんが、積分時間0.01秒のときの、範囲であらわされる、代表周波数というのもおかしな表現ではありません。
このグラフは、ジェット戦闘機のタイプや、速度など操縦の仕方で、変化すると考えられますし、このグラフのように、マイクとの位置関係でも、とりうる値が変化します。
高い代表周波数の分析には、短い積分時間の設定が必要です。また(低域などを押さえる)A特性(人間の聴覚の性能をシミュレートしたフイルター特性)が人間の聴覚上の感覚をあらわしている代表周波数分析には必要です。
ここで、次の音響パラメーターに移ります。
1.Φ(0)真の音圧レベルはA特性を加味して積分時間単位の音響エネルギーを計算します。
2.測定積分時間を、それぞれの人間の脳の時定数(反応速度、音圧レベルを計算する平均時間)に合わせてやれば、
Φ(0)真の音圧レベルはA特性を加味した時定数単位の音響エネルギーですから。
騒音の個人個人に対する真の音圧レベルということができます。
Φ(0)のグラフです。Y軸に音圧レベル、X軸が測定経過時間です。
。
2004年8月9日加筆終了。
January 2002 by Masatsugu Sakurai