| Japanese | English |
アコースティックギターをチューニング
(楽器のチューニング-1)
RA(リアルタイムアナライザ)を使って、アコースティックギターのチューニングを試みました。
シグナルジェネレータ
ギターをケースから出したのは何年ぶりでしょうか。昔は、A(ラ)の音叉(440Hz)で5弦を合わせ、それを基準に他の弦をチューニングしていました。

音叉で膝を叩いてギアーの胴体に当てて共鳴させます。音叉とずれているとウヮンウヮンとうねりが出るので、それをポーンというひとつの音になるように弦の張り具合を調整するわけです。ところが音叉は長い間、響いているわけではないので、チューニングに馴れないうちは何度も膝を叩くことになって痛かったです。(苦笑)
そこで音叉の代わりに「シグナルジェネレータ」を使ってみましょう。
パソコンのスピーカーからポーっという440Hzの音が出るので、5弦をそれに合わせます。音叉とちがって、ずっと鳴り続けているので慌てる必要がありません。
リアルタイムアナライザ
たしかに、音叉が見当たらないときには「シグナルジェネレータ」が使えると便利ですが、別の方法も考えてみましょう。
まず思いつくのが「オシロスコープ」です。リアルタイムな波形が表示されるものですから、周波数のちがいもわかります。
「シグナルジェネレータ」で440Hzの正弦波を鳴らしながら、ギターの5弦を弾きます。そもそもパソコンの内蔵スピーカーでは(音質の問題で)波形が正弦波に見えません。マイクもワンポイントステレオマイクですからパソコンとギターに振り分けることができません。ギターの弦を弾いても下図のような波形になってしまいます。
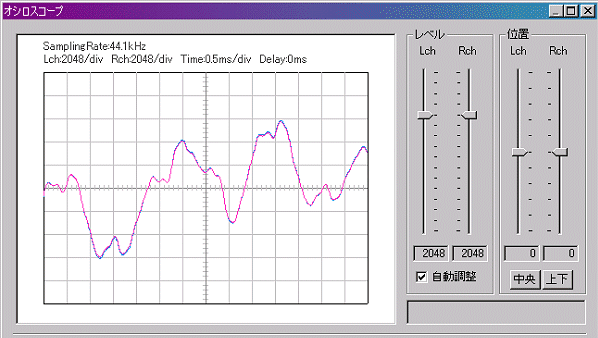
「
2掃引オシロスコープ」同様、左右のチャネルを独立して使ってみましょう。ここではUSBオーディオインターフェイス(ROLAND
UA-5※)と、SONYのマイクミキサーを使って、Lチャネルは440Hzの正弦波を、Rチャネルはマイクで拾ったギターの音を表示させました。
※下の写真ではUA-5ではなくUA-3という機材を使っていますが、この機材はトラブルが多く報告されており、お薦めできません。UA-5の方は動作確認が取れています。

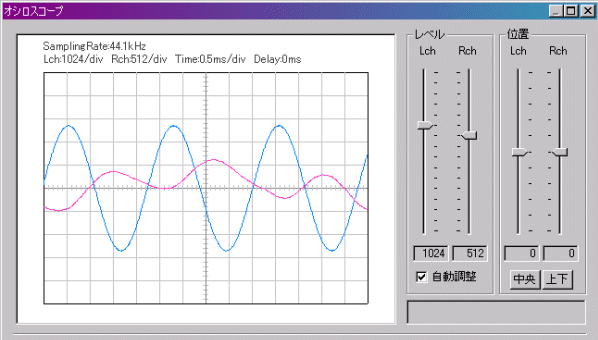
青が「シグナルジェネレータ」の出力をそのまま戻した波形、赤がギターの音です。青はぴたっと静止していますが、赤は(音がすぐに減衰するせいもあって)一定しません。そもそもギターの音は単純な正弦波ではありませんから、オシロスコープでチューニングするのは無理があるようです。
それでは「パワースペクトル」を見てみましょう。グラフを見やすいように「周波数範囲」を100~1,000Hzに設定してあります。
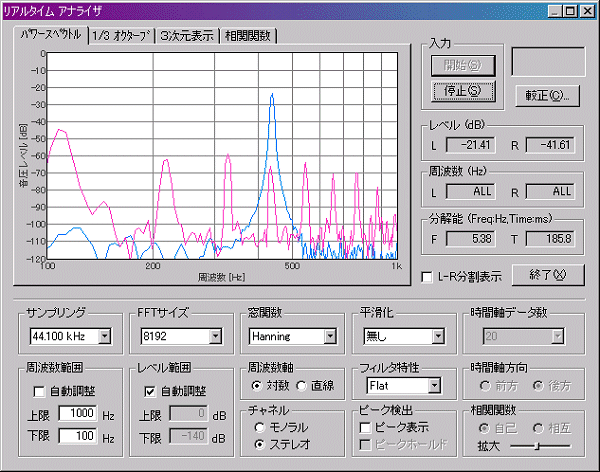
青のグラフは440Hzがはっきりと出ているのに対して、赤は440Hz以外にも前後に多くの倍音が出ています。これでは基準音に対する微妙なチューニングのちがいを読み取るのはむずかしいです。
それでは「相互相関」関数で見てはどうでしょうか。「リアルタイムアナライザ」の「相関関数」タグを選択し、ウィンドウ右下の「相関関数」を「相互」にセットします。
「相互相関」とは「左右の耳に到達する信号の類似度を表す関数」です。Lチャネルの正弦波信号だけではグラフは0のままで下図のように波形は出ません。
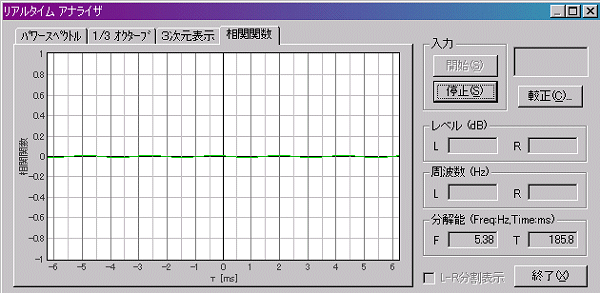
そこにRチャネルからギターの音を入れてやるとAの音に反応しました。それが下図です。
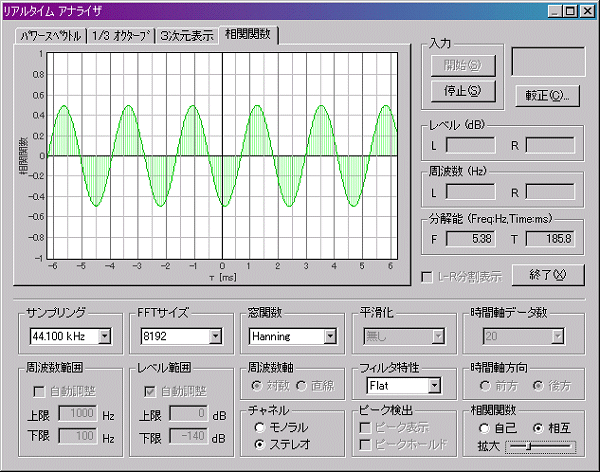
チューニングが微妙にずれていると、上図のような波形が右か左に流れます。ぴったりと合うと静止するのでチューニングが合ったことがわかります。
RA(リアルタイムアナライザ)の「相互相関」機能を使って、アコースティックギターのチューニングができることがわかりましたが、相互相関は5弦開放(A)だけでなく、4弦開放(D)にも反応するのです。機材は前回同様、Lチャネルに440Hzの正弦波、Rチャネルにマイクから拾ったギターの音を入力してあります。計測ソフトはDSSF3の英語版を使用していますが、もちろん日本語版でも同様に使えます。
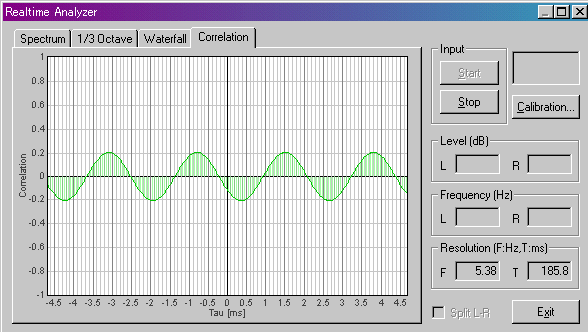
5弦開放の「1/3オクターブ」です。青が440Hzの正弦波の信号、赤がギターの音です。多くの倍音を含んでいます。
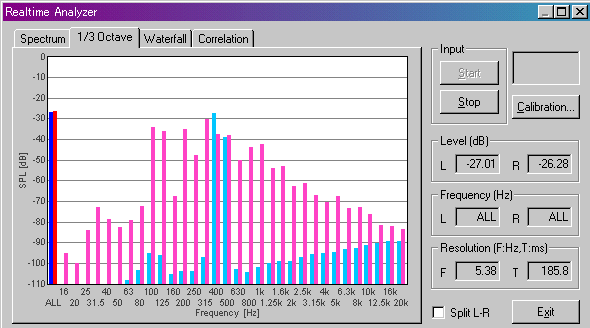
5弦開放(A)の「パワースペクトラム」です。
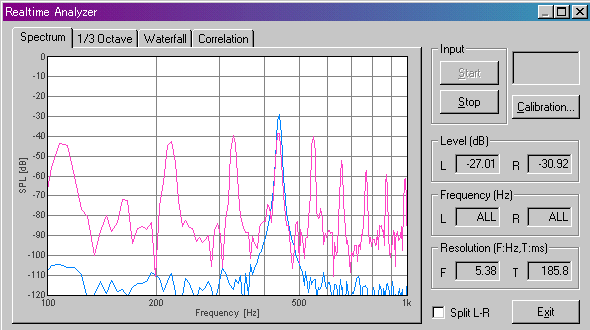
4弦開放(D)の「パワースペクトラム」です。440Hzを含んでいるので「相互相関」で反応があったのです。
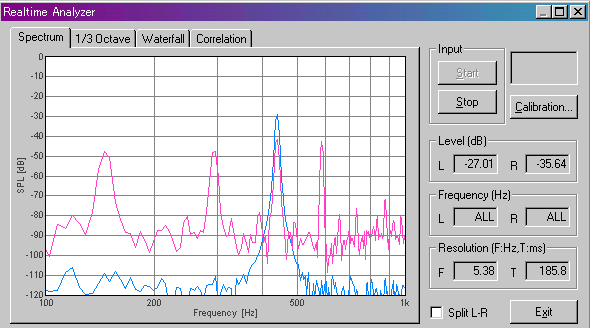
つぎに平均律音階の周波数を示します。平均律とは、1オクターブは12の半音で構成されているため、基音に2^(1/12)をかけていく音階です。
| 音階 |
平均律(Hz) |
| A |
440.0 |
| A# |
466.1 |
| B |
493.8 |
| C |
523.2 |
| C# |
554.3 |
| D |
587.3 |
| D# |
622.2 |
| E |
659.2 |
| F |
698.4 |
| F# |
739.9 |
| G |
783.9 |
| G# |
830.6 |
| A |
880.0 |
上表によるとDの周波数は587.3Hzです。たしかに「パワースペクトラム」にもその周波数が出ています。Dの倍音であれば587.3Hzの整数倍(あるいは整数分の1倍)のはずですから、それ以外の音も出ていることになります。
振動数比が1:2の2音は1オクターブ、2:3の2音は5度、3:4の2音は4度です。2音が簡単な整数の比になると和音として協和します。587HzのDからみると440HzのAは4度にあたります。5弦開放(A)の「パワースペクトラム」グラフを見ても、4度にあたる330Hzが強く出ていることがわかります。
これがギター特有のものなのかどうかを確かめるために、ピアノのAとDの「パワースペクトル」を見てみましょう。
これがピアノのAです。
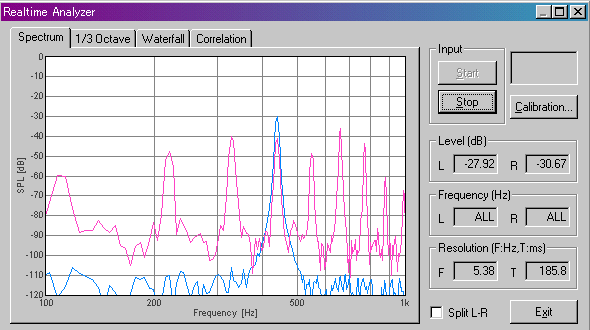
これがピアノのDです。
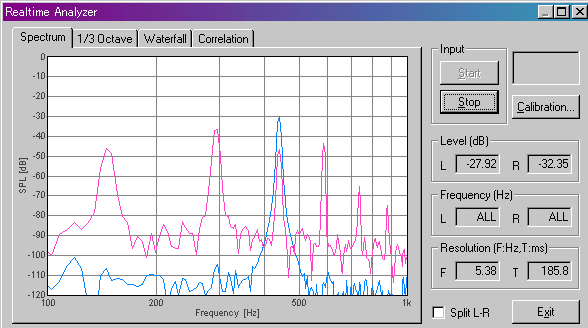
ギターと比べるとそれぞれの強さは異なりますが似ています。ピアノのDにも440Hzが含まれているようです。
そうすると「RAを使った楽器チューニング法」としては、まず「シグナルジェネレータ」で基音(この場合はA)のトーンを出しながら大体合わせてから「相互相関」で微調整するということになります。
November 2002















