| Japanese | English |

基本周波数、フォルマント周波数と自己相関の関係
（日本語音声の分析2）

以降は2002年の分です。2004年加筆分は　その記述があるところからです。

今回は「あ」の発音について前回より精密な積分時間10mseで、発音からランニングステップ5msecづつ分析を行います。

音声データ： voice1.wav (44.1kHz / Stereo / 2.78sec / 480KB)

▼　発声5 msec後　（実験開始後　0.29秒）

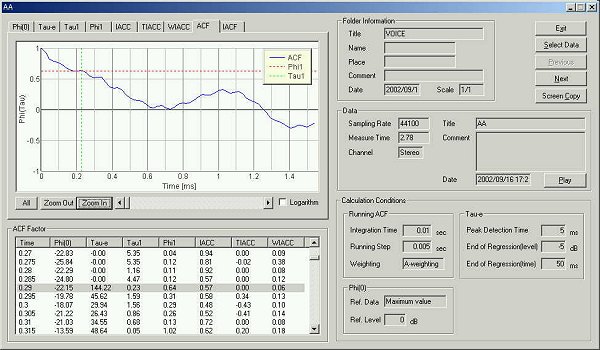
τe　144.22 msec　発声からピークパワーまでの上昇過程でのτeは大雑把には減少していきます。

自己相関の波形を眺めると、0.23、0.34、0.41、0.55、0.68，0.91，1.02，1.11、… msecにそれぞれ角張ったところがあります。これもスペクトラムのピーク周波数に対応しているようです。

▼　発声10 msec後　（実験開始後　0.295秒）

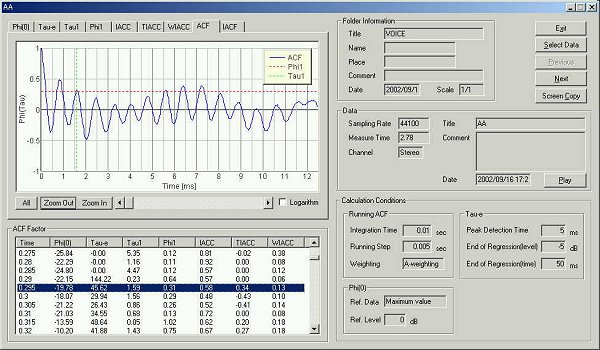
ここでのτeは46.62 msecです。発声中では一番長いものです。ただしこれから（発声からピークパワーまでの上昇過程での）τeは減少していきます。

拡大図

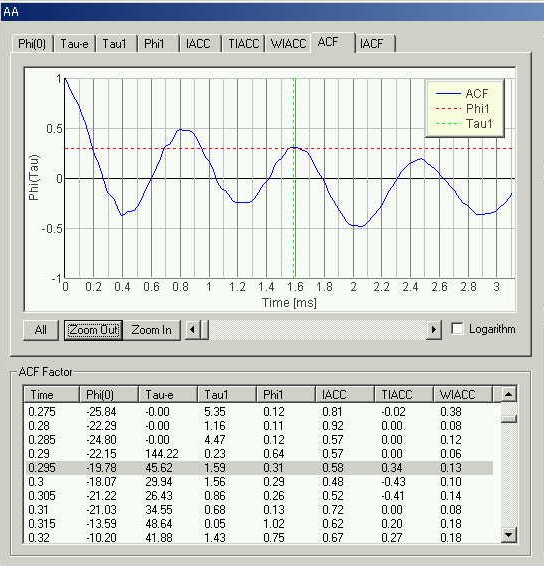
上図をみると自己相関ACFのピークの遅れ時間は0.8 msecです。　さらに基本周波数　5～8 msecに低い山があり、はっきりしません。この段階では、時間が早すぎて（10/1000秒しかたっていない）必要な周波数の音が認識できていないため基本周波数が分析されていないと考えられます。今回は基本周波数の取得にはこの倍の20 msecかかりました。

0.8　フォルマント周波数　1000/0.8＝1250 Hz

▼　発声15 msec後　（実験開始後　0.3秒）

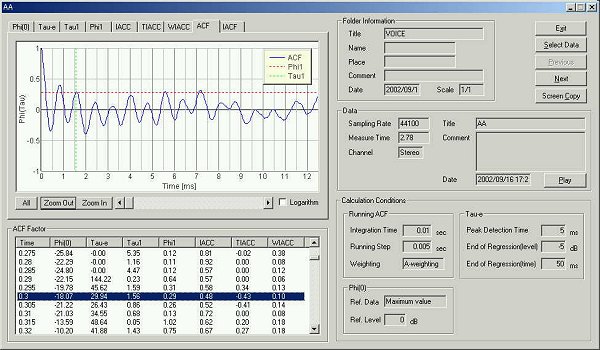
τe　29.94 msec、発声からピークパワーまでの上昇過程でのτeが2番目に小さいポイントです。ピークは0.8、1.56 msec　 基本周波数　5～8 msecに低い山

同拡大図

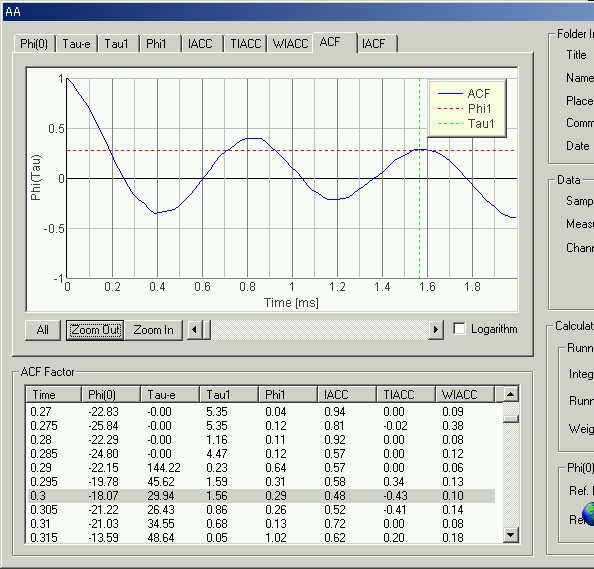
0.8 msec　フォルマント周波数　1000/0.8＝1250 Hz

▼　発声20 msec後　（実験開始後　0.305秒）

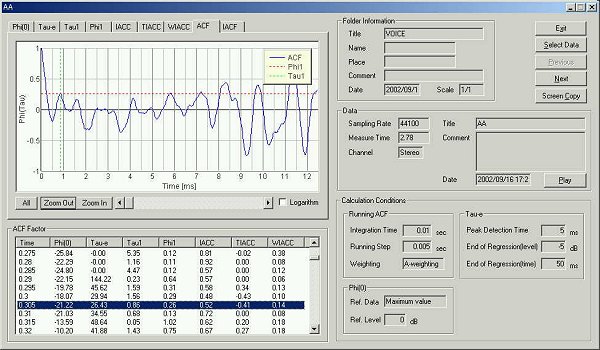
前に比べて音響パワーが -3dB下がっています。最初にためらいがあります。発声者が自らの発声の音程を確かめているのかもしれません。

τe　26.43 msec　発声からピークパワーまでの上昇過程でのτe　最小のポイント

パワーを出す方向に発声中であり、その中でτe最小のポイントは最も運動の変化が大きいときを表しますが、そこは自己相関のピークが、フォルマント周波数をあらわすポイントになっています。また、基本周波数が認識できたポイントです。音声スペクトラムは低域に行くほど、エネルギーが大きくなるスペクトラムです。音響エネルギーの大きな低域を扱ったためとも考えられます。

0.86 msec　　基本周波数　8.35 msec　119 Hz

同拡大図

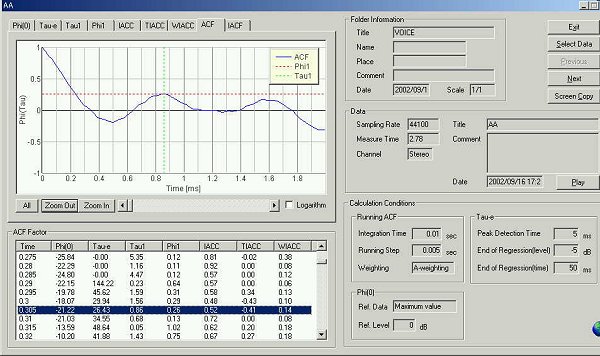
0.86 msec　フォルマント周波数　1000/0.86=　1162 Hz

▼　発声25 msec後　（実験開始後　0.310秒）

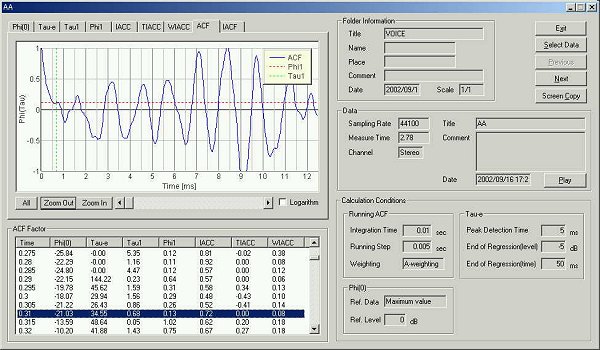
τe　34.45 msec
0.68、1.61　　　基本周波数　　8.39 msec　119 Hz

前のピークよりも後ろの1.61 msecのときのピークのほうが大きいのは、フォルマント周波数のピッチの強さを持つものがふたつ存在し、その周波数の間が離れていて、エネルギー的に連続ではないことを意味しています。もし連続しているなら、ふたつのフォルマント周波数はひとつの山のなかで連続したピークを持ちます。この場合、低いフォルマント周波数を検知したために発生しました.

同拡大図

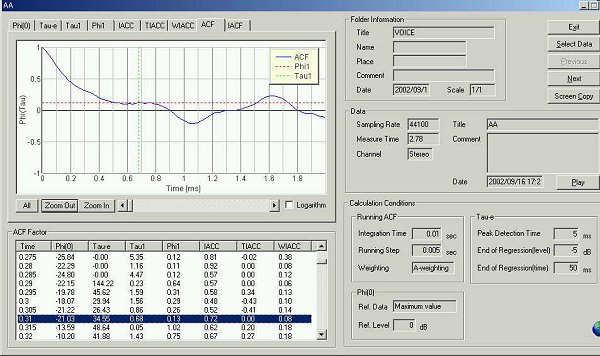
フォルマント周波数は一番低い周波数を第1フォルマント（F1）として、以後F2、F3と続きます。

マイナスの最初のピークは　1.05 msec　952 Hz　第2フォルマント（F2）

1.3 msec　フォルマント周波数　1000/1.3=769 Hz　新第1フォルマント（F1）

1.61 msec　フォルマント周波数　1000/1.63=613 Hz　旧第1フォルマント（F1）

613 Hzはこの段階の第1フォルマント周波数ですが、すこしピークが低いため過渡的な（このあと消える）ACFと考えられます。このACFは「あ」のパワースペクトラムを特徴的にあらわしているといえます。

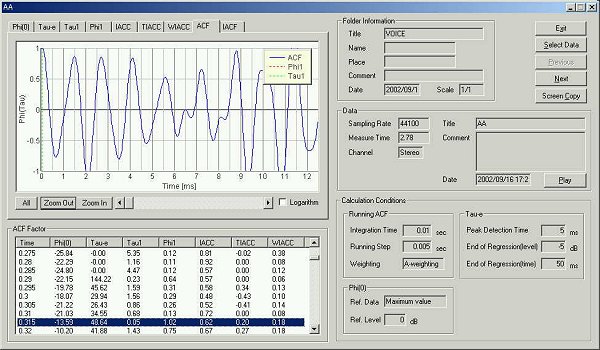
τe　48.64 msec、ACF　　1.5、基本周波数　　8.8 msec　113 Hz

1.5 msec　フォルマント周波数　　666 Hz

▼　発声35 msec後　（実験開始後　0.32秒）

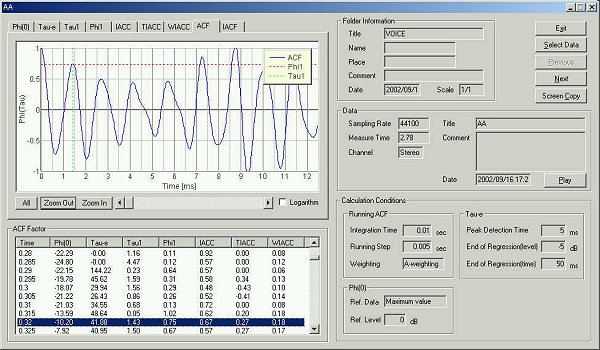
τe　41.88 msec、ACF　1.43、基本周波数　8.75 msec　114 Hz

1.43 msec　フォルマント周波数　699 Hz

▼　発声75 msec後　（実験開始後　0.36秒）

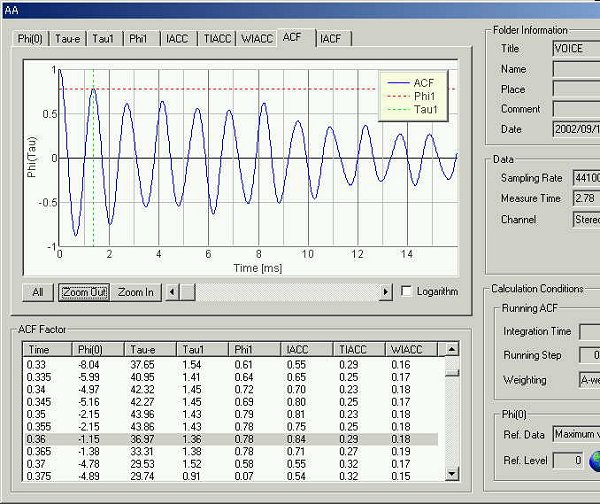
τe　36.97 msec
前のデータからからこの最後のデータまでの 50 msecのτeはいずれもほとんど同じ値42～43 msecでした。

ACF 1.36　フォルマント周波数　735 Hz、基本周波数　8.21　121 Hz

音響パワーレベルの時間変化。赤点が同タイム、音響パワーのピークポイントです。

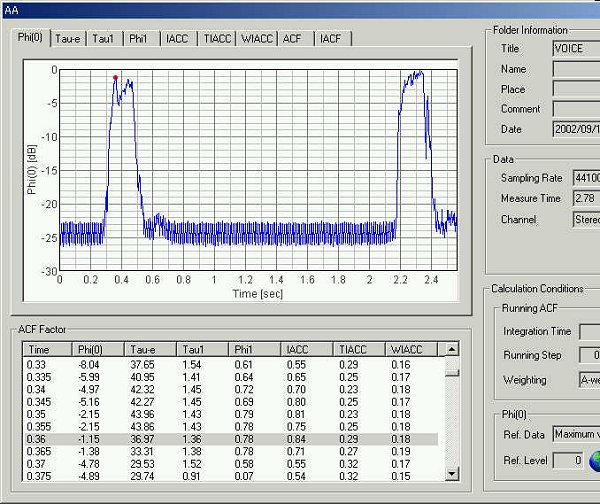
今回は音圧レベルの時間的変化を精密に分析した場合のACFの関数からえられるフォルマントや、基本周波数などを調べました。

この5msecごとの分析では、基本周波数は20 msec後に第3-第2フォルマントは25msec後までに、発声後30 msecで第1フォルマント660～736 Hzを見つけることができました。　

ここまで　2003年4月分

ここから2004年7月加筆分

この測定では、人間の会話のなかで言語は、たくさんの情報をすばやく伝えることができる点に着目しています。いったいどれくらい早口が許されるだろう。聴くほうでは、どれくらいの時間で、聞き取れるのだろうかなどです。

確かに音を聞き分ける程度に聞くのであれば、言葉の並びからも、推測できますし、文の意味や、繰り返し使われる言葉などの認識は、初めての言葉より容易ですし。　聞く人のなれも在るでしょう。

この場合は、”あ”という意味の無い発音の認識ですから、意味のある音のつながりとは、認識の仕方が違うはずです。

たとえばこの2003年の測定では、”あ”の発生を発生開始から　5msec ごとの分析を行い。人の耳が、”あ”という発音だと認識できる瞬間を探しています。この場合、ひとつの発音を複数のフォルマント周波数、（第１、第２など）で、聞き分けるとすれば、ＤＳＳＦ３は開始から、どのくらいの時間で、それを分析できるかを調べています。　

今回は、新開発の、高時間解像度なＦＦＴ分析で、スペクトラム成分の時間応答を調べます。

積分時間を短くして、５msec くらいにします。２００Ｈｚ以下は基本周波数で、認識する必要ないからです。フォルマントの５００Ｈｚ以上でほとんど音声認識は出来るでしょう。そして時間を計るために1/1000 秒に細かくランニングステップを変更します。ランニングステップはすごく増えましたが、積分時間が非常に短くなったので、　分析速度はこちらも速くなるでしょう。

2004年7月16日　加筆分

これは日本語音声分析３の女性の発音です。間違えてそれを分析してしまいました。というのは、2年もたって、忘れていたからです。ただ、今読み返してみると女性の音声分析で、。この条件はやってないので、良かったと思います。

このページの音声ＷＡＶＥファイルを読み込んで、再分析を行えば、男性の声の分析が出来ますが。今となっては女性の声の分析を消して、男性の声に戻すのも、意味が無いし。

この分析の後に、まったく同じやり方で、男性の声の分析を行うのも、冗長です。そこでしませんのでもし、興味があるかたはやってみて下さい。

2004年7月16日　加筆分終了

ＷＡＶＥ表示で、測定開始後　1.408秒を指定して、スペクトラムアナライザー表示を行います。確かに５００ＨＺ以上が表示されていますが、表示がはっきりしません。というより、ＦＦＴ分析やスペクトラム表示は、非常に短時間の分析や信号変化を主体には分析できないのです。短い平均時間では位相の影響を受けてしまいます。音響信号は振幅を持つ波だからです。そのためＦＦＴ分析はあくまで、正弦波信号のような、時間的に連続に続く波の分析です。

以下のＡＣＦの分析のほうは、同じ条件で、3.6ｍｓｅｃの位置の２７７Ｈｚの基本周波数表示をはじめとして、大方”あ”のフォルマントが確認できる。Ｘ軸方向０から3つを先頭からの3つのピークで1.5ｍｓｅｃまでにあらわしています。次にＸ軸方向に拡大してその値を確認してみます。

Ｘ軸方向に32倍に拡大してみました。最初のピークは0.27ｍｓｅｃあたり、３７００Ｈｚあたりこれはピーク周波数でしょう。次の0.85msecは１１７６Hz、次は1.13ｍｓｅｃこれは８８４Ｈｚ　この同じようなピークが１１７６ＨＺと、８８４Ｈｚにあるのが、”あ”の特徴でしょう。この場合、第１フォルマントが８８４Ｈｚで第２フォルマントが１１７６Ｈｚです。

目的がフォルマントの発見であれば、このランニングＡＣＦ分析からのフォルマントの発見は効率がいい。一方ＦＦＴ分析はといえば積分時間が充分に長いときは、ＡＣＦ分析の前にスペクトラムを使用して確認を取る必要があるくらい、ＦＦＴ分析は安定している。このわけは簡単だ。なぜなら長時間測定、平均するからである。

2004年7月　加筆終了

April 2003 by Masatsugu Sakurai