| Japanese | English |
自己相関関数入門
みなさんが中学・高校で習ってきたように、音は音源から伝わる空気の圧力の変化であり、その圧力変化は波形として表すことができます。音は時間の経過とともに伝わるものであり、時間が存在しなければ私たちは音を聞くことも楽しむこともできません。ここでまず、これから述べる“自己相関関数”は時間の領域から音に迫るものであることを覚えておいてください。
音の時間領域と周波数領域
音を記述する方法は２つあり、１つは時間に基づいて記述する方法（振幅と時間を軸にとった“波形”）、もう１つは周波数に基づいて記述する方法（振幅と周波数を軸にとった“スペクトル”）です。この２つは同じものを記述しており、１つの記述法からもう１つの記述法へ変換すること、またその逆変換が可能です。つまり音はどちらを用いても同じように効果的に記述できますが、そのときによって、どちらかの方法が便利になってきます。たとえば、普段みなさんがコンポなどで目にする周波数分布を表すグラフ（スペクトル）は、重低音や高音がどれだけ含まれているかをひとめで分かるよう記述したものです。
音と私たちの脳の関係
音は音波すなわち物理現象としての音と、聴覚すなわち感覚としての意味の両面を持っています。私たちの耳に入ってきた音は聴覚路に沿って進み、時間の流れとともに知覚されます。このとき、音の持つ意味は時々刻々脳によって解釈されます。ここに音を時間領域で解析することの重要性があります。音の時間領域における特徴を表す自己相関関数は、数学的にはスペクトルと同じ情報を持っていますが、私たちの脳における信号処理の過程を考慮しているという点で、スペクトルによる解析と大きく異なります。
自己相関関数とは
では、音の時間的特徴を表す自己相関関数（ACF: autocorrelation
function）はどのように表されるのでしょうか。
音源から発せられた音源信号を時間関数p(t)とすると、ACFは次式で定義されます。
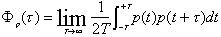・・・・(1)
ここで、tは遅れ時間、2Tは積分区間です。また、先に説明したように、時間領域と周波数領域における記述法は互いに変換が可能であり、音源信号のパワースペクトルをPd(w)とすると、ACFは以下のように得られます。
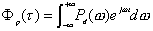・・・・(2)
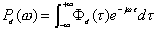・・・・(3)
このように、ACFとパワースペクトルは数学的に同じ情報を含んでいます。
ACFを数式で表すと式（１）のようになりますが、この物理的な意味を考えてみましょう。
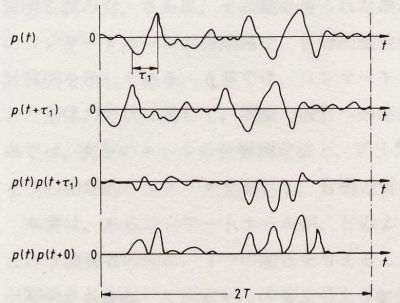
図１ τ＝０および、τ＝τ１における音源信号の自己相関関数の物理的意味
図１のように、積分区間2Tの長さの信号p(t)を切り出すと、時間tだけ遅れた信号はp(t+t)となります。もしp(t)とp(t+t)の振幅が大きく、同様な繰り返し成分があれば、２つの信号の相関値Fp(t)は大きくなります。すなわち、ACFは信号自体にどの程度の類似性があるかを表す関数といえます。
以下に、音楽と騒音のACFの例を示してみましょう。
▼ 音楽
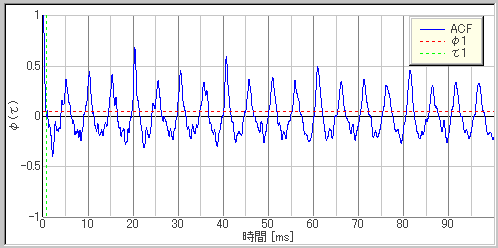
▼ 騒音
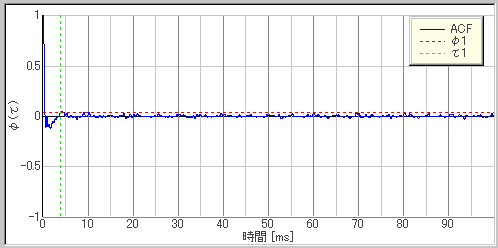
音楽に比べて、騒音はACFの値があっという間に小さくなっています。これは、騒音には様々な音が含まれているため、類似性が低くなるということを表しています。
自己相関関数のファクター
次に、上のようにして得られた自己相関関数（ACF）の波形から何が分かるのかを説明したいと思います。これまでに、ACFに含まれる重要なパラメータとして、次の４つのファクターを用いて、様々な音の解析が行われています。
（１）遅れ時間が０のときのエネルギー Fp(0)
音のパワーを表し、特に音の大きさに関する心理量であるラウドネスと関係があります。
（２）ACF有効継続時間 te
正規化ACFのエンベロープが0.1になる遅れ時間で定義され、音源信号自体に含まれる繰り返し成分あるいは残響成分を表します。
正規化ACFは次式で定義されます。
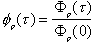・・・・(4)
（３）第１ピークの遅れ時間 t1
音の高さに関する心理量であるピッチとの関連があると考えられます。
（４）第１ピークの振幅 f1
主にピッチの強さと関連があると考えられます。
自己相関関数から抽出されるファクターτe (繰り返し成分の継続時間)
の定義
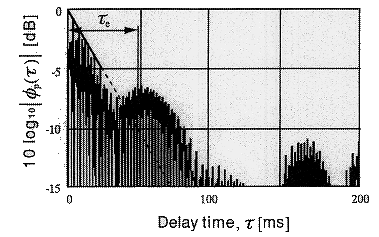
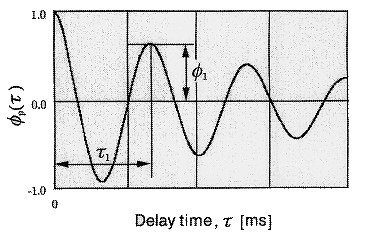
自己相関関数から抽出されるファクターτ1 (音のピッチ)
およびφ1 (音のピッチの強さ) の定義
自己相関関数を使うと
自己相関関数から抽出されるファクターはそれぞれ音の心理的な評価との関連が深いことが分かってきています。たとえば建築音響の分野では、ある音楽を音源信号としたとき、その信号の自己相関関数から抽出されるファクターを用いることによって、その音楽を聴く際に最も適した反射音の遅れ時間や残響時間を予測することができます。これにより、心地よい音楽を楽しむことのできるコンサートホールの設計が可能となります。
また、様々な音源信号の特徴を自己相関関数から抽出されるファクターによって表すことができることから、さまざまな音が存在する屋外での騒音測定の際に、ある特定の音だけを記録したい場合などに、これらのファクターが有効となる、など様々な応用例が考えられます。
