A Computational Software for Identification of Noise - an Application for Car Engines

Masatsugu Sakurai
 Yoshimasa Electronic Inc., 1-58-10 Yoyogi, Shibuya, Tokyo 151-0053 Japan

Identification results of noise from car engine using a computational system are described here. The concept of the system is based on the model of human auditory-brain system [1], which includes the autocorrelation function (ACF) and interaural crosscorrelation function (IACF) mechanisms and the specialization of the human cerebral hemispheres. The system consists of the software of a laptop computer, and a receiver with dual channel microphones. The software is developed to measure the physical factors in noise fields and the characterization of the regional environment noise. There are four orthogonal factors extracted from the ACF of the noise source, F(0), te, t1 and f1. Also there are three spatial factors, IACC, tIACC, and WIACC. These factors may be utilized for the identification of the noise source as a timbre difference. Results show that the identification of the noise sources of different car-engines made here is satisfactory.



INTRODUCTION

This study is not conventional static analysis, but dynamic one. The characteristics of engine noise are found by analysis using the Real-time Analyzer System. Since these characteristics can be rephrased as the characteristics of engine itself, it seems possible to identify them experientially. The purpose of this study is to develop the technology that can identify them exactly using the parameters extracted from the autocorrelation function on personal computer. (Figure 1) It was embodied in system which measures environment noise automatically for a long time and identifies its noise source.



FIGURE 1. (a) An example of the calculation of the effective duration, te, from normalized ACF by linear fitting to the initial envelope of the ACF. (b) Definitions of f1 and t1 for the ACF.




OUTLINE OF THE MEASUREMENT SYSTEM

The measurement system consists of software that is used to calculate the ACF and IACF factors from real-time noise data, a laptop computer, and two microphones arranged as a binaural pair. (Figure 2) The source code for the program was written in C and the program was developed under Windows NT, 2000. The amount of main memory restricted the maximum interval for a single session to about 30 s at a sampling frequency of 44.1 kHz. For calculations of a running ACF and running IACF, an integration interval (2T) [2], and running step which is the period for a single calculation of 2T, have to be set up before the measurement. Real-time extraction of all orthogonal factors from the ACF and IACF was achieved by the system. For further information on the system, refer to our web site [3].

FIGURE 2. A block diagram of the system for measuring environmental noise.




ALGORITHM FOR SOURCE IDENTIFICATION USING THE FACTORS OF THE ACF

The distances between values of each factor at (te)min for the unknown target data are calculated, to find the total distance for the identification for a target source. Values of template are obtained as a typical example of a target source. [4]

(1)
(2)


EXAMPLES OF ACF FACTORS FROM THE NOISE OF CAR ENGINES

Noise from the engines of four different cars (cars A-D), as shown in Table 1, was measured by using the system. Two microphones were set 1 m apart, to the right and in front of each car. The distance between two microphones was 20 cm, and the microphones were set up 1.0 m above the ground. Measurements were in open air, and in fine weather. The analysis for each engine started just after the engine was started. The noise sources for each car were analyzed over 3.0 s. The conditions for this analysis of the ACF are listed in Table 2. Orthogonal factors were obtained after the signals were passed through the A-weighting network. As an example of parameters extracted from the autocorrelation function of engine noise, which ware obtained by the measurement system, the data of t1 are shown in Table 3.

Table 1. The car engines measured.
Car Engine displacement (cc) Cylinders
A 2746 Straight 6
B 5547 V8
C 1990 Straight 6
D 3405 V8

Table 2. Conditions for analysis running ACF (a), and for obtaining te (b).
(a)
Calculation of the running ACF
 Integration interval (2T) 0.2 s
 Running step 0.1 s

(b)
Calculation of te
 Time interval for detecting ACF peaks 1 ms
 Maximum decay level of regression -10 dB
 Maximum delay time of regression 20 ms

Table 3. Results of measured t1 for Cars A-D at (te)min and at two other local minima of te, and the average values with standard deviation (SD) over the whole period.
t1 [ms] Values at (te)min Values at local minima of te Average (SD)
A 0.70 0.70 0.70 0.72 (0.02)
B 1.22 1.25 1.20 1.31 (0.11)
C 0.77 0.73 0.75 0.76 (0.02)
D 0.68 0.70 0.68 0.67 (0.03)


CONCLUSION

The different physical characteristics of four different car engines are reflected strongly in the ACF orthogonal factors. Thus, the computational system described here should be quite useful for describing the characteristics of environmental noises. Such a noise can be identified by using four factors extracted from ACF; F(0), te, f1, and t1. In particular, the ACF factors which were obtained at (te)min are good indicators of differences in the subjective evaluation of the noise source and the noise field [5, 6].



ACKNOWLEDGEMENT

The author would like to thank Mr. Shinichi Aizawa for his invaluable assistance with programming the software. This work is supported by the Research and Development Applying Advanced Computational Science and Technology Program of the Japan Science and Technology Corporation (ACT-JST), 1999.


REFERENCES

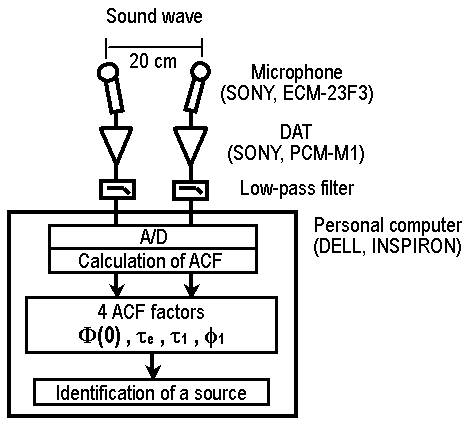
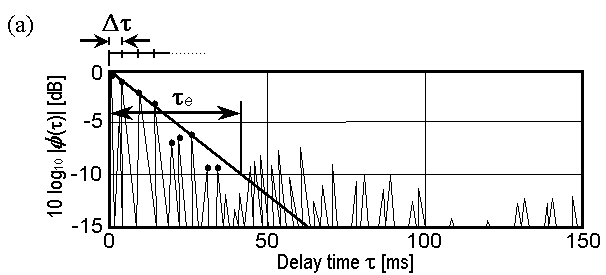
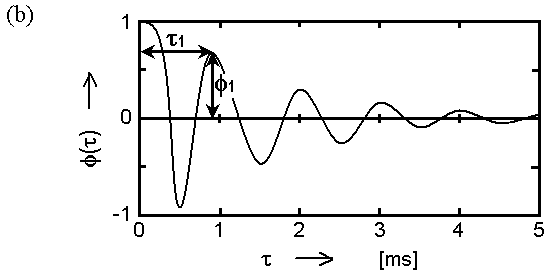
1. Ando, Y., Architectural Acoustics -Blending Sound Sources, Sound Fields, and Listeners-, New York, AIP Press/Springer-Verlag, 1998.
2. Mouri, K., Akiyama, K. and Ando, Y., Journal of Sound and Vibration 241, 87-95 (2001).
3. Web site of Yoshimasa Electronic Inc. (URL: http://www.ymec.co.jp/)
4. Sakurai, M., Sakai, H. and Ando, Y., Journal of Sound and Vibration 241, 19-27 (2001).
5. Ando, Y., Okano, T. and Takezoe, Y., The Journal of the Acoustical Society of America 86, 644-649 (1989).
6. Mouri, K., Akiyama, K. and Ando, Y., Journal of Sound and Vibration 232, 139-147 (2000).